Back in August of this year, the game Among Us leapt in popularity. A social game where crewmates try to complete tasks while staying alive. At the same time, impostors try to kill off the innocent players while also sabotaging the crew. It’s a fun, interactive twist on in person social games such as Werewolf or Mafia.
With the interactive gameplay, rounds end when a player reports a dead body or call an emergency meeting and the remaining players get a chance to discus and potentially vote out one player.
This got me thinking, ignoring the various strategies for the game, and avoiding where impostors kill off innocent players, if players were just removed/voted off randomly, what would be the odds of a crewmate or an impostor victory, and with that, the expected win rate overall.
Calculating the probabilities under these assumptions isn’t too difficult, but designing a simulation to do this is also very straightforward. First, let’s simulate a single Among Us game.
It’s important to understand the victory criteria for the crewmates and impostors in this setup. The crewmates win this way when all the impostors have been voted off before the number of crewmates gets reduced to the same number of remaining impostors. The standard game is with 10 players, with two of them being impostors. We can write a function in R that takes in variables for the number of players and number of impostors and then returns a 1 if the crewmates win, and a 0 if the impostors win.
library(tidyverse)## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──## ✓ ggplot2 3.3.3 ✓ purrr 0.3.4
## ✓ tibble 3.1.2 ✓ dplyr 1.0.6
## ✓ tidyr 1.1.3 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.1## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()amongusGame <- function(players = 10, impostors = 2) { # return 1 on crewmate victory
crewmates <- players - impostors
while (crewmates != impostors & impostors != 0) {
voted <- sample(c("impostor", "crewmate"), 1, prob = c(impostors, crewmates))
if (voted == "impostor") {
impostors <- impostors - 1
} else {
crewmates <- crewmates - 1
}
}
if (impostors == 0) {
return(1)
} else {
return(0)
}
}Now that we have a function that simulates a single game, we can simply write a wrapper function to repeat it an arbitrary number of times, as well as compute the odds of crewmates winning this way.
amongusSim <- function(players = 10, impostors = 2, N = 2000){
results <- vector(mode = "logical", length = N)
for (i in 1:N) {
results[i] <- amongusGame(players, impostors)
}
return(results)
}Now, we can have a bit of fun by visualizing what the perceived win rate is based on how many games it has been since we started to count. We can make a basic line graph for this.
amongusPlot <- function(players = 10, impostors = 2, N = 2000){
winresults <- amongusSim(players, impostors, N)
print(sum(winresults)/N)
winrate <- vector(mode = "logical", length = N)
for (i in 1:length(winresults)) {
winrate[i] <- sum(winresults[1:i])/i
}
ggplot(tibble(gamenum = 1:N, winrate = winrate), aes(x = gamenum, y = winrate )) + geom_line() + xlab("Game #") + ylab("Win Rate") + ylim(0,1)
}amongusPlot()## [1] 0.5975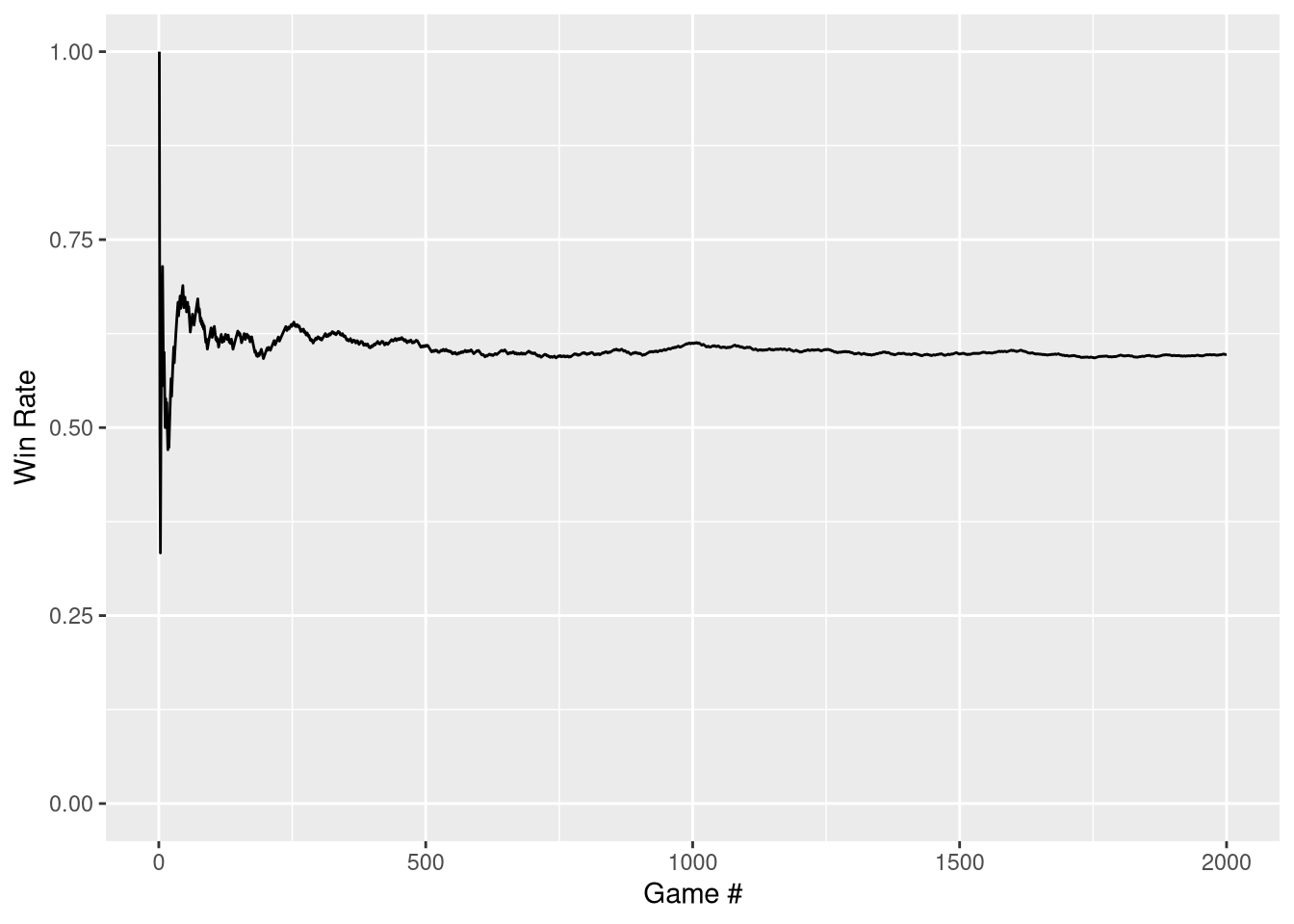
We can see that from about 1000 onward, the result seems to arrive at 0.6
So apparently randomly voting for a player gives the crewmates a slight advantage. From this we can then calculate what the expected win rate of each player if every game was played this way.
(0.6)∗0.8+(0.4)∗0.2=0.56
Which means just by guessing randomly, including players voting for themselves, everyone would win about 56% of their games.
Of course, this is just an exercise in odds, given the game is much more complex than these assumptions (like the impostors would never vote for themselves or their fellow impostor), especially when looking at the various strategies that can be employed.