So, after my last Dungeons and Dragons post, I got asked about the Advantage/Disadvantage mechanic in Dungeons and Dragons Fifth Edition, so let’s look into that a bit.
In D&D, to succeed at a task, you roll a 20-sided die(d20) and with some math and checking with your Dungeon Master (DM), you determine if you succeed or not. In previous editions you would add your character’s modifier, as well as any additional bonuses or penalties due to the specific scenario. Fifth edition got rid of that except for one specific case, and instead replaced it with Advantage/Disadvantage.
Simply put, if your character is in some sort of advantageous situation when attempting a task, you get Advantage. In a disadvantageous situation? Disadvantage. If you were in a combination of scenarios providing at least one advantage and one disadvantage then you just attempted normally. For a normal situation you roll your d20, then add your character’s relevant ability modifier and proficiency bonus if applicable. For Advantage, you roll your die twice, taking the higher result before adding in your modifiers. Disadvantage is the same, except you take the lower result.
This simplifies and streamlines things a lot for the DM, and instead of needing to memorize a bunch of rules and their modifiers, you just need to memorize those rules. From there it’s easy to reason out if you get Advantage or Disadvantage.
Of course, this has gotten many people wondering how this compares to a modifier to the roll. The answer is not so straightforward, as you’ll see that it depends upon the target result you need to succeed. First, let’s populate a tibble with Results, their Probabilities, and the Probability for beating or exceeding a result. This will include regular, Advantage, and Disadvantage.
library(tidyverse)## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──## ✓ ggplot2 3.3.3 ✓ purrr 0.3.4
## ✓ tibble 3.1.2 ✓ dplyr 1.0.6
## ✓ tidyr 1.1.3 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.1## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()library(ggthemes)
advdisdf <- expand.grid(list(1:20,1:20))
maxvals <- apply(advdisdf, 1, function(x) max(x))
minvals <- apply(advdisdf, 1, function(x) min(x))
advdistdf <- tibble(R1 = advdisdf$Var1, R2 = advdisdf$Var2, Advantage = maxvals, Disadvantage = minvals)
AdvP <- summary(as.factor(advdistdf$Advantage))/400
DisP <- summary(as.factor(advdistdf$Disadvantage))/400
ACDF <- rev(cumsum(rev(AdvP)))
DCDF <- rev(cumsum(rev(DisP)))
RegP <- summary(as.factor(1:20))/20
CDF <- seq(1,0.05,by = -0.05)
ADPMF <- tibble(Result = 1:20, AdvP, ACDF, DisP, DCDF, RegP, CDF)Let’s plot what looks a bit like a “leaf”, showing the increase in probability of beating a result with Advantage or beating a result with Disadvantage.
ADPMF %>%
ggplot() +
geom_line(aes(x = Result, y = ACDF), size = 2) +
geom_line(aes(x = Result, y = DCDF), size = 2) +
geom_ribbon(aes(x = Result, ymin = CDF, ymax = ACDF), fill = "green4", alpha = 0.5) +
geom_ribbon(aes(x = Result, ymin = DCDF, ymax = CDF), fill = "red4", alpha = 0.5) +
geom_line(aes(x = Result, y = CDF), size = 2) +
xlab("d20 Target") +
ylab("Odds of result equaling or exceeding target") +
theme_solarized()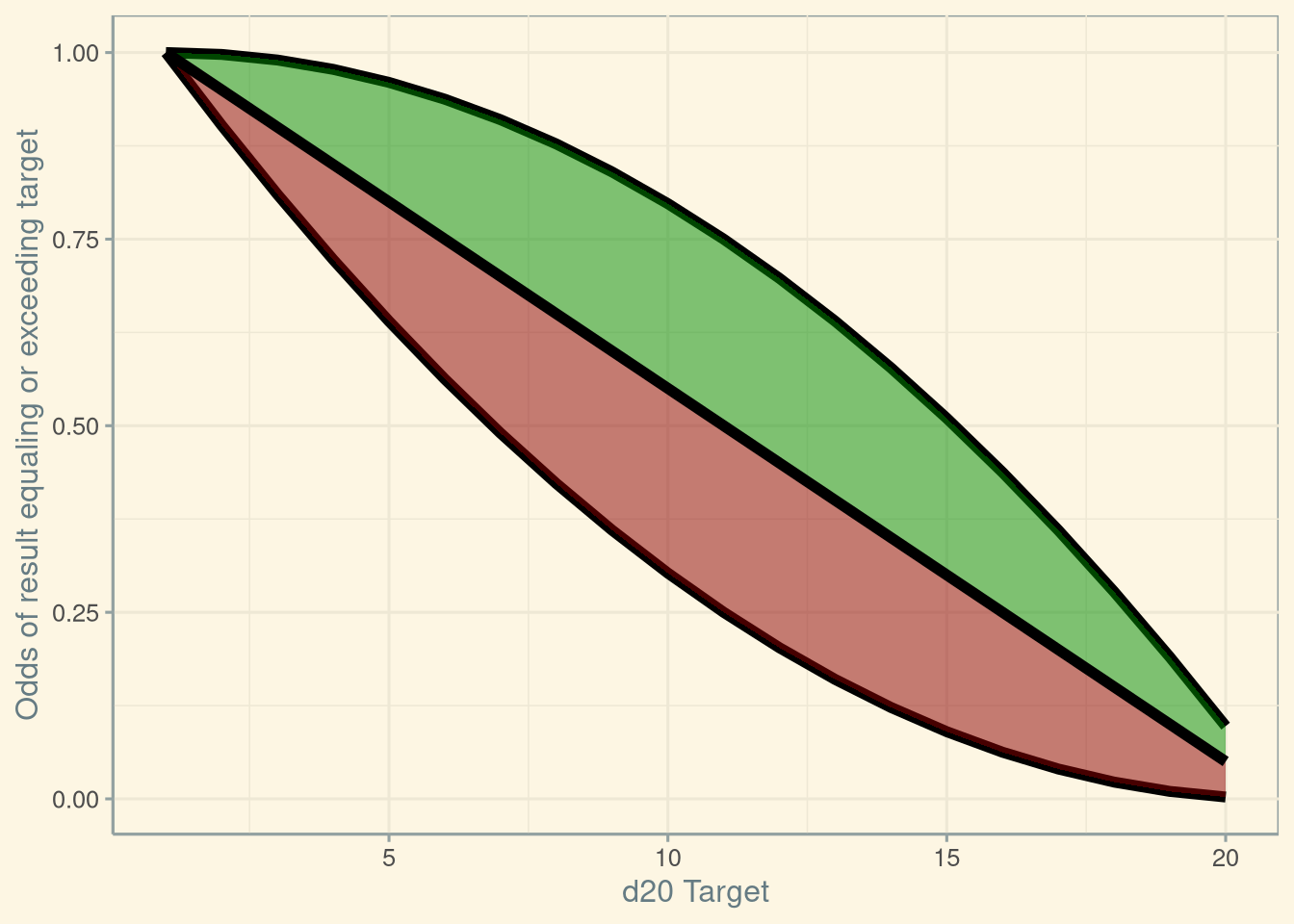
We see here that at the extreme ends the bonus or penalty is not very large, but at 11 the bonus or penalty is much larger, exceeding ±5. Let’s quantify the bonus or penalty and visualize it.
ADPMF$Advantage <- (ADPMF$ACDF - ADPMF$CDF)/0.05
ADPMF$Disadvantage <- (ADPMF$DCDF - ADPMF$CDF)/0.05
ADPMF %>%
gather(`Advantage`, `Disadvantage`, key = "category", value = "Bonus") %>%
select(Result, category, Bonus, ACDF, CDF, DCDF) %>%
ggplot(aes(x = Result, y = Bonus, fill = category)) +
geom_bar(stat = "identity", dodge = "position", alpha = 0.5) +
xlab("d20 Target") +
ylab("Effective Bonus") +
scale_fill_manual(values = c("green4", "red4")) +
theme_solarized() +
scale_y_continuous(breaks = -5:5, minor_breaks = -5:5) +
scale_x_continuous(breaks = seq(0,20, by = 5), minor_breaks = 1:20) +
ylab("Effective bonus modifier")## Warning: Ignoring unknown parameters: dodge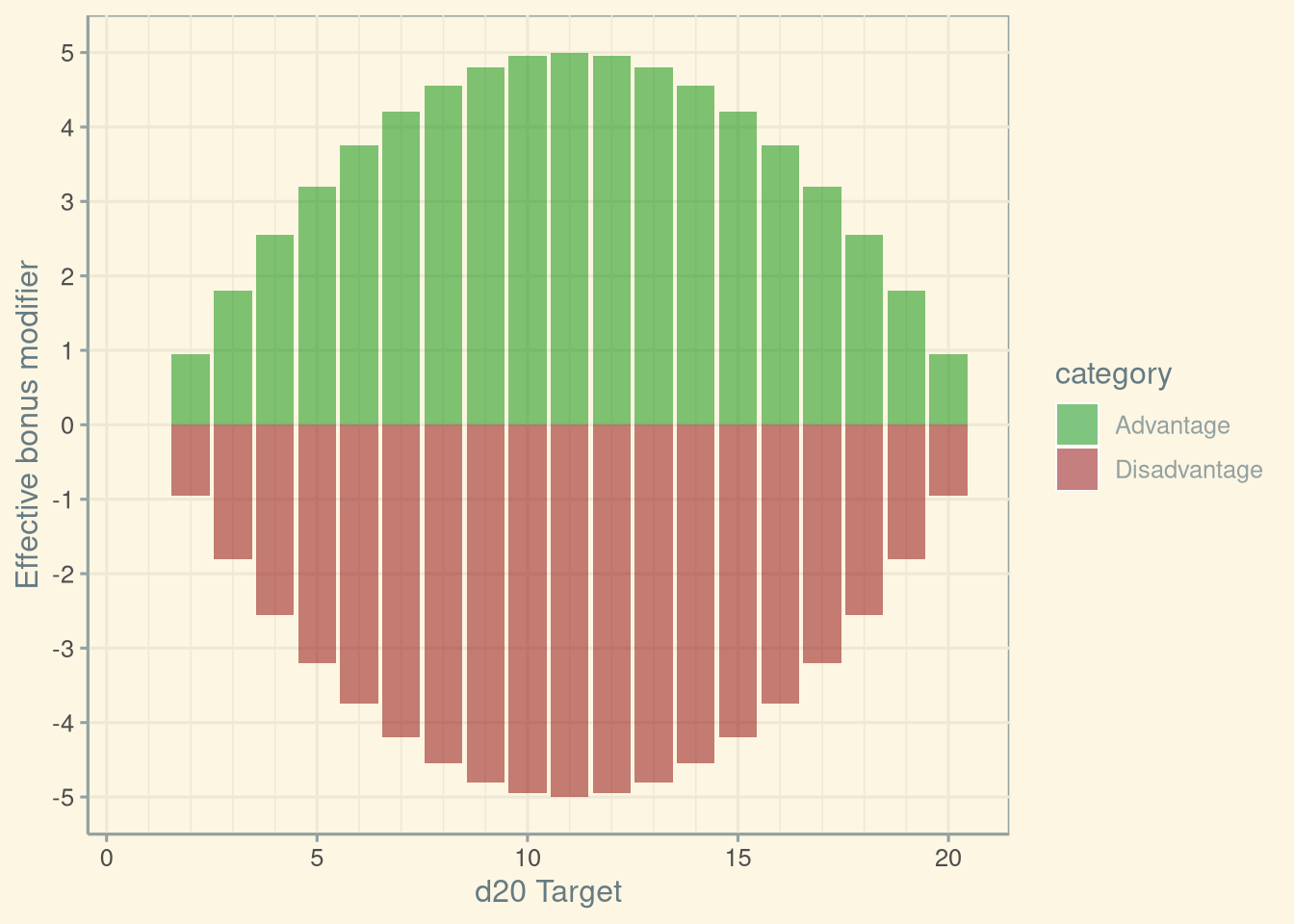
Here we can see more clearly the greatest change is when the target of the roll is 11, and it gets smaller as it becomes more extreme.
Now, my question was not just on Advantage, but how granting Advantage compared to bonus damage on an Attack. As it turns out, this can get pretty complex based on the varied kinds of attacks there are, their damage dice etc. So let’s look at a small set of situations.
Let’s assume we have a 1st level player. Like all level 1 characters, they have a +2 proficiency bonus, and let’s assume that their ability modifier for their weapon attack and damage is +3, the highest you could have with the Standard Array. Under this situation I will look at each of the different weapon’s damage dice. This gives a total bonus to hit of +5 (+2 proficiency bonus plus their +3 ability modifier), so we’ll look at targets with AC of 7 to 24 (AC 6 and below has the same odds of hitting as an AC 7 for someone with a +5, as well as anything higher than AC 24 will be equally hard to hit as AC 24).
First, let’s calculate the average damage per attack. That means taking the odds of getting a regular hit times the average damage for a regular hit plus the odds of getting a critical hit times the average damage from a critical hit. First let’s make some tables for this for Advantage and under regular circumstances
toHit <- 5
damagePlus <- 3
ACRange <- 7:24
Target <- ACRange - toHit
avgDieDamage <- c(2.5, 3.5, 4.5, 5.5, 6.5, 7)
AdamageResults <- matrix(nrow = length(Target),ncol = length(avgDieDamage))
RdamageResults <- matrix(nrow = length(Target),ncol = length(avgDieDamage))
for (i in 1:length(Target)) {
for (j in 1:length(avgDieDamage)) {
AdamageResults[i, j] <- sum(ADPMF$AdvP[as.character(Target[i]:19)]) * (avgDieDamage[j] + damagePlus) + ADPMF$AdvP['20'] * (2*avgDieDamage[j] + damagePlus)
RdamageResults[i, j] <- sum(ADPMF$RegP[as.character(Target[i]:19)]) * (avgDieDamage[j] + damagePlus) + ADPMF$RegP['20'] * (2*avgDieDamage[j] + damagePlus)
}
}Then we can calculate the difference, and visualize it:
Aboost <- as_tibble(AdamageResults - RdamageResults)## Warning: The `x` argument of `as_tibble.matrix()` must have unique column names if `.name_repair` is omitted as of tibble 2.0.0.
## Using compatibility `.name_repair`.colnames(Aboost) <- c("1d4", "1d6", "1d8", "1d10", "1d12", "2d6")
Aboost$AC <- ACRange
Aboost %>%
gather(`1d4`, `1d6`, `1d8`, `1d10`, `1d12`, `2d6`, key = "damageDice", value = "bonusDamage", factor_key = T) %>%
ggplot(aes(x = AC, y = bonusDamage, fill = damageDice)) +
geom_bar(stat = "identity", position = "dodge") +
xlab("AC of Target") +
ylab("Averge damage increase per attack") +
scale_fill_manual(name = "Damage Dice",
labels = c("1d4", "1d6", "1d8", "1d10", "1d12", "2d6"),
values = c("#b58900", "#dc322f", "#6c71c4", "#268bd2", "#2aa198", "#859900")) +
theme_solarized()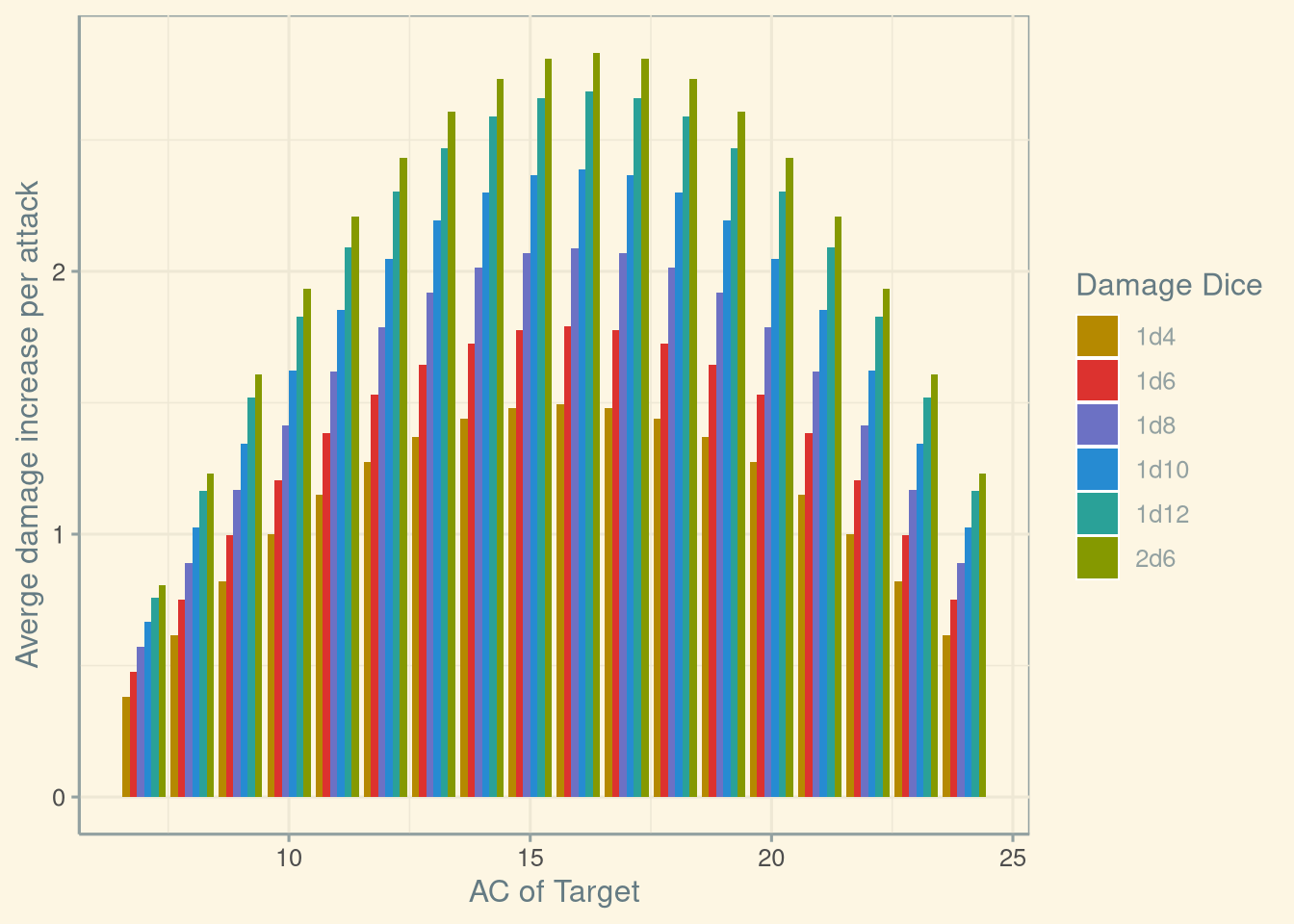
Something that I notice right away, is that for a given Damage Dice, the shape of the curve follows the bonus to succeed from Advantage.
Now, this wasn’t exactly the question. To answer this, I need to calculate additional tables for the regular scenario, but with varying bonuses to damage. I do this from a +1 to +13 damage. I compare each of these, along with the Target AC and the Damage Dice type to find the closest amount of bonus damage to the effective increase from having Advantage.
AdamageResults2 <- rep(list(matrix(nrow = length(Target),ncol = length(avgDieDamage))), 13)
DdamageResults2 <- rep(list(matrix(nrow = length(Target),ncol = length(avgDieDamage))), 13)
RdamageResults2 <- rep(list(matrix(nrow = length(Target),ncol = length(avgDieDamage))), 13)
closestMatrix <- matrix(nrow = length(Target),ncol = length(avgDieDamage))
bonusMatrix <- matrix(nrow = length(Target),ncol = length(avgDieDamage))
for (k in 1:13) {
for (i in 1:length(Target)) {
for (j in 1:length(avgDieDamage)) {
RdamageResults2[[k]][i, j] <- sum(ADPMF$RegP[as.character(Target[i]:19)]) * (avgDieDamage[j] + damagePlus + k) + ADPMF$RegP['20'] * (2*avgDieDamage[j] + damagePlus + k)
if (k > 1) {
if (abs(AdamageResults[i, j] - RdamageResults2[[k]][i, j]) < abs(closestMatrix[i, j])) {
closestMatrix[i, j] <- RdamageResults2[[k]][i, j] - AdamageResults[i, j]
bonusMatrix[i, j] <- k
}
} else {
closestMatrix[i, j] <- RdamageResults2[[1]][i, j] - AdamageResults[i, j]
bonusMatrix[i, j] <- 1
}
}
}
}
Aboost2 <- as_tibble(bonusMatrix)
colnames(Aboost2) <- c("1d4", "1d6", "1d8", "1d10", "1d12", "2d6")
Aboost2$AC <- ACRange
Aboost2 %>%
gather(`1d4`, `1d6`, `1d8`, `1d10`, `1d12`, `2d6`, key = "damageDice", value = "bonusDamage", factor_key = T) %>%
ggplot(aes(x = AC, y = bonusDamage, fill = damageDice)) +
geom_bar(stat = "identity", position = "dodge") +
xlab("AC of Target") +
ylab("Damage bonus equivalent to gaining Advantage") +
scale_fill_manual(name = "Damage Dice",
labels = c("1d4", "1d6", "1d8", "1d10", "1d12", "2d6"),
values = c("#b58900", "#dc322f", "#6c71c4", "#268bd2", "#2aa198", "#859900")) +
scale_y_continuous(breaks = seq(0,15, by = 5), minor_breaks = 0:15) +
theme_solarized()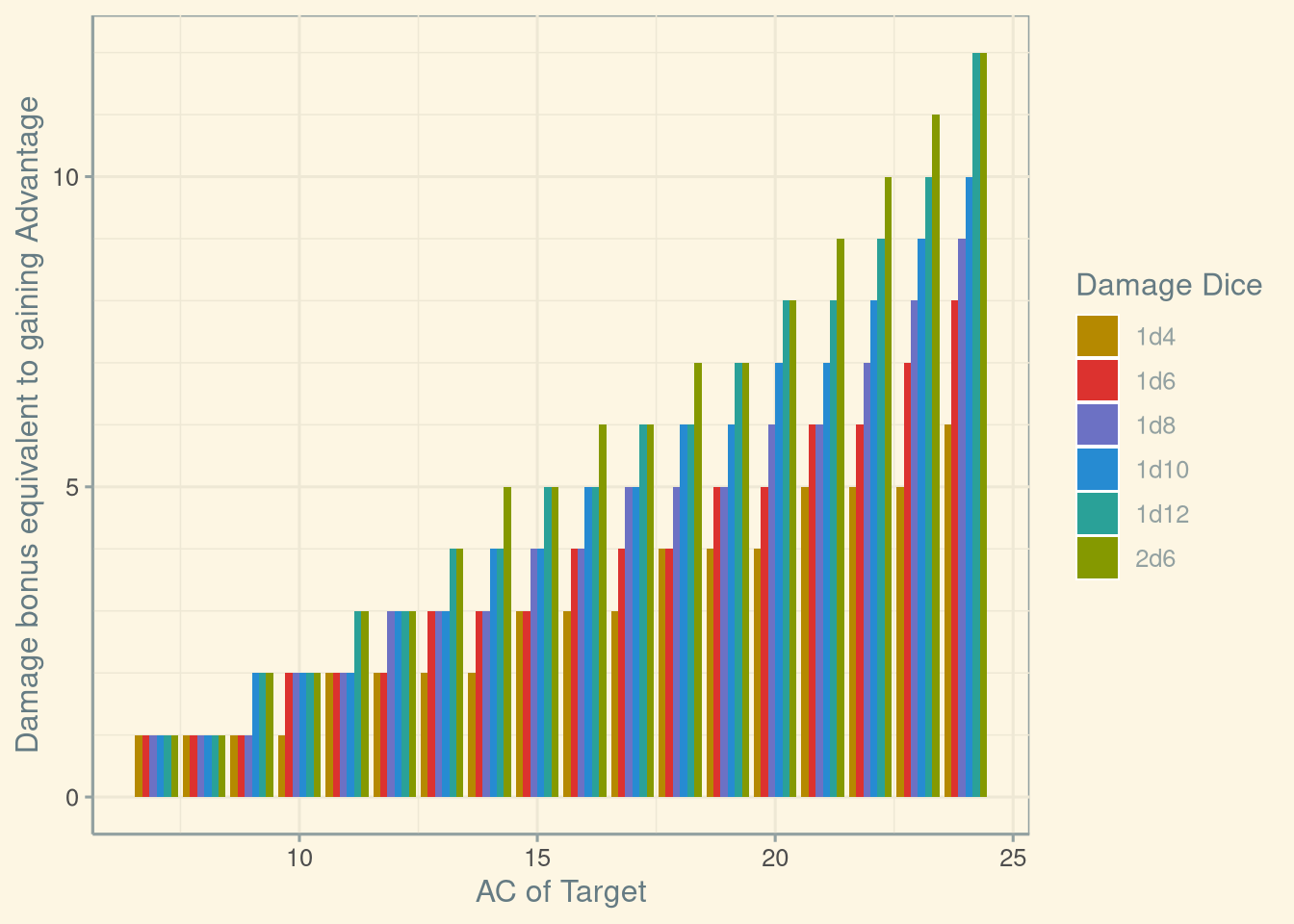
Now, this initially surprised me, as it is a monotone increasing result. However, as I got to thinking about it, it made more sense to me. Initially as you go from low to mid AC targets, your bonus to hit is substantial with Advantage, so you need to keep on getting a greater damage bonus to equal the average damage per attack. However, as these numbers go higher, a greater proportion of the average damage per round with advantage comes from critical hits, which provides a significant effective damage boost.
Now, looking at these graphs, a player or DM may ask how they can use them. The first three illustrate well how the Advantage mechanic influences results, both success and failure. When it comes to designing adventures, some DMs will focus on making sure the players feel like they are getting things done, that they succeed a large enough portion of their ability checks and attack rolls, adding to encounters in other ways to balance the game out. In this case, you can make your players feel even more epic by liberally granting Advantage when their target is around 11, as it makes it all the more epic to succeed. Similarly, failure through Disadvantage can help bring tension in a task of similar difficulty.
As for the final graph, this is more of a look at the internals of one of the core mechanics of Fifth edition Dungeons and Dragons, and how someone might get a similar result by going a different way. Personally, I think the Advantage/Disadvantage mechanic is an elegant solution to rewarding/punishing characters for their circumstances in a fun and easy way.